仿射变换

仿射变换是指图像可以通过一系列几何变换来实现平移、缩放、旋转等操作。OpenCV中为仿射变换提供的仿射函数为cv2.warpAffine()，可以通过一个映射矩阵M来实现这种变换。其中，M具体可为：

\[ {\rm dst}(x, y) = {\rm src}(M_{11}x + M_{12}y + M_{13}, M_{21}x + M_{22}y + M_{23}) \]

一般格式：

1
dst = cv2.warpAffine(src, M,dsize[, flags[, borderMode[, borderValue]]])
  • dst表示仿射后的输出图像，类型与原始图像相同。
  • src表示要仿射的原始图像。
  • M表示变换矩阵。
  • dsize表示输出图像尺寸的大小。
  • flags表示插值方法，默认INTER_LIEAR。
  • borderMode表示边类型，默认BORDER_CONSTANT。
  • borderValue表示边界值，默认为0。

平移

平移是对象位置的移动。如果我们想要将\((x，y)\) 偏移至并\((tx,t_y)\)，我们可以创建转换矩阵\(M\)如下：

\[ M = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \end{bmatrix} \]

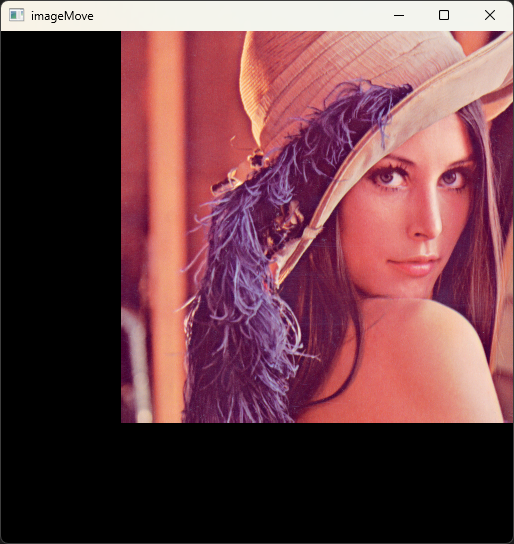
当想将原始图像向右上移动120个像素时，矩阵\(M\)可以为：

\[ M = \begin{bmatrix} 1 & 0 & 120 \\ 0 & 1 & -120 \end{bmatrix} \]

例如：

1
2
3
4
5
6
7
8
9
10
import cv2 as cv
import numpy as np
image = cv.imread("pic/lena.png")
h,w = image.shape[:2]  # 获取图像大小信息
M = np.float32([[1, 0, 120], [0, 1, -120]])  # 构建转换矩阵
imageMove = cv.warpAffine(image, M, (w, h))  # 平移
cv.imshow("image", image)  # 显示原始图像
cv.imshow("imageMove", imageMove)  # 显示变换后的图像
cv.waitKey()
cv.destroyAllWindows()
屏幕截图 2025-01-21 160629.png

缩放

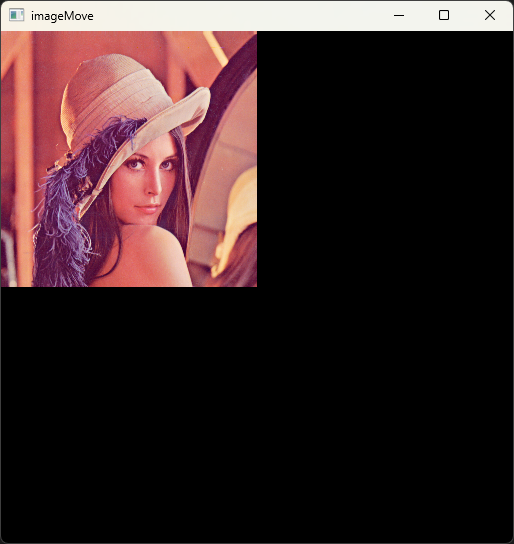
当想将原始图像缩小为一半时，矩阵\(M\)可以为：

\[ M = \begin{bmatrix} 0.5 & 0 & 0 \\ 0 & 0.5 & 0 \end{bmatrix} \]

例如：

1
2
3
4
5
6
7
8
9
10
import cv2 as cv
import numpy as np
image = cv.imread("pic/lena.png")
h,w = image.shape[:2]  # 获取图像大小信息
M = np.float32([[0.5, 0, 0], [0, 0.5, 0]])  # 构建转换矩阵
imageMove = cv.warpAffine(image, M, (w, h))  # 缩放
cv.imshow("image", image)  # 显示原始图像
cv.imshow("imageMove", imageMove)  # 显示变换后的图像
cv.waitKey()
cv.destroyAllWindows()
屏幕截图 2025-01-21 161030.png

旋转

在OpenCV中，当进行旋转操作时，可以通过函数cv2.getRotationMatrix2D()得到仿射变换函数cv2.warpAffine()的转换矩阵。其一般格式为：

1
ret = cv2. getRotationMatrix2D(center, angle,scale)
  • center是旋转的中心点。
  • angle表示旋转角度，正数为顺时针旋转，负数为逆时针旋转。
  • scale表示变换尺度。

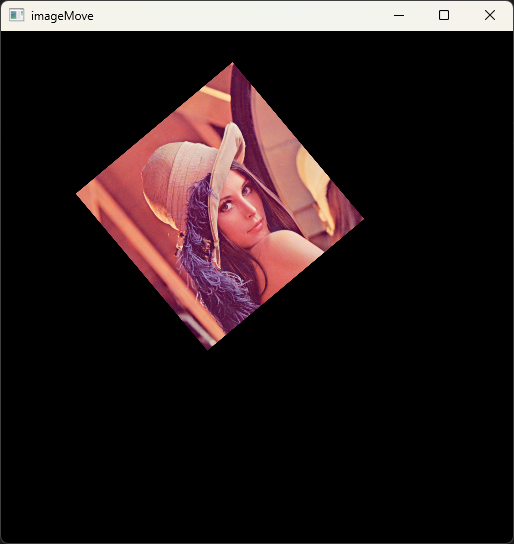
例如，要将图片缩小至原来的0.4后，逆时针旋转40°：

1
2
3
4
5
6
7
8
9
10
import cv2 as cv
image = cv.imread("pic/lena.png")
h, w = image.shape[:2]  # 获取图像大小信息
# 得到转换矩阵M，效果是以图像的宽高的1/3为中心点顺时针旋转40°，缩小为原来的0.4
M = cv.getRotationMatrix2D((w/3, h/3), 40, 0.4)
imageMove = cv.warpAffine(image, M, (w, h))  # 进行仿射变换——旋转
cv.imshow("image", image)
cv.imshow("imageMove", imageMove)
cv.waitKey()
cv.destroyAllWindows()
屏幕截图 2025-01-21 162052.png

重映射

将一幅图像内的像素点放置到另一幅图像的指定位置，这个操作过程叫作重映射。重映射通过修改像素点的位置得到一幅新图像。因此，在构建一幅新图像时，需要确定新图像中每个像素点与原始图像所对应的位置。所以，映射函数的作用就是查找新图像像素在原始图像内的位置。OpenCV中的cv2.remap()函数提供了十分方便的自定义重映射方式。其一般格式如下：

1
dst = cv2. remap(src, map1, map2, interpolation[, borderMode[, borderValue]])
  • dst表示目标图像。
  • src表示原始的图像。
  • map1表示点(x, y)的一个映射或者点(x, y)的x值。
  • map2表示的值与map1有关。当map1表示点(x, y)的一个映射时，map2为空；当map1表示点(x, y)的x值时，map2表示点(x, y)的y值。
  • interpolation表示插值方式。
  • borderMode表示边界模式。
  • borderValue表示边界值，默认为0。

注意 mapl和map2的值都是浮点数，所以目标图像可以映射回一个非整数的值，这意味着目标图像可以映射到原始图像中不存在像素值的位置。此时，函数中的interpolation参数可以控制插值方式对图像进行插值操作。

复制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import cv2 as cv
import numpy as np
#  构建一个6×6的随机数组
image = np.random.randint(0, 256, size=[6, 6], dtype=np.uint8)
w,  h = image.shape  # 得到数组的宽与高
# 建立新数组的大小
x = np.zeros((w, h),  np.float32)
y = np.zeros((w, h),  np.float32)
# 实现新数组的访问操作
for i in range(w):
   for j in range(h):
        x[(i, j)] = j
        y[(i, j)] = i
rst = cv.remap(image,  x,  y,  cv.INTER_LINEAR)  # 数组的复制
#  打印输出结果
print("image=\n", image)
print("rst=\n", rst)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
image=
 [[177  38 121 254 235 172]
 [174 128 158  69  15 229]
 [143  23  36 125  61 195]
 [ 86 202 202  60  78  17]
 [192 111 113  47  23  99]
 [149 239  11  19 210 251]]
rst=
 [[177  38 121 254 235 172]
 [174 128 158  69  15 229]
 [143  23  36 125  61 195]
 [ 86 202 202  60  78  17]
 [192 111 113  47  23  99]
 [149 239  11  19 210 251]]

通过remap()函数实现图像的复制：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import cv2 as cv
import numpy as np
image = cv.imread("pic/lena.png")  # 读取一幅图像
w, h = image.shape[:2] # 得到图像的宽与高
# 建立新图像的大小
map1 = np.zeros((w,h), np.float32)
map2 = np.zeros((w,h), np.float32)
# 实现新图像的访问操作
for i in range(w):
    for j in range(h):
        # 访问图像
        map1[(i, j)] = j
        map2[(i, j)] = i
rst = cv.remap(image, map1, map2, cv.INTER_LINEAR)  # 图像复制
# 显示图像
cv.imshow("image", image)
cv.imshow("rst", rst)
cv.waitKey()
cv.destroyAllWindows()

绕x轴旋转

图像绕着x轴翻转，在数学上是指映射过程中x坐标轴的值保持不变，y坐标轴的值以x轴为对称轴进行交换。使用remap()函数实现时，map1的值保持不变，map2的值设置为“总行数-1-当前行号”，这是由于OpenCV中行号的下标是从0开始决定的。

例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import cv2 as cv
import numpy as np
# 构建一个6×6的随机数组
image = np.random.randint(0, 256, size=[6, 6], dtype=np.uint8)
w, h = image.shape # 得到数组的宽与高
# 建立新数组的大小
x = np.zeros((w, h), np.float32)
y = np.zeros((w, h), np.float32)
# 实现新数组的访问操作
for i in range(w):
    for j in range(h):
        x[(i, j)] = j
        y[(i, j)] = w - 1- i
rst = cv.remap(image, x, y, cv.INTER_LINEAR) # 数组绕x轴翻转
# 打印输出结果
print("image=\n", image)
print("rst=\n", rst)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
image=
 [[204 212  30 213 107 247]
 [103 121 174  81 214 247]
 [218 203 119  69 170 143]
 [ 18 151 183   0   0 126]
 [ 89 170 103  69 161 118]
 [229 176  62 240  99  33]]
rst=
 [[229 176  62 240  99  33]
 [ 89 170 103  69 161 118]
 [ 18 151 183   0   0 126]
 [218 203 119  69 170 143]
 [103 121 174  81 214 247]
 [204 212  30 213 107 247]]

绕y轴旋转

图像绕着y轴翻转，在数学上是指映射过程中y坐标轴的值保持不变，x坐标轴的值以y轴为对称轴进行交换。使用remap()函数实现时，map2的值保持不变，map1的值设置为“总列数-1-当前列号”，这是由于OpenCV中列号的下标是从0开始决定的。

例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import cv2 as cv
import numpy as np
# 构建一个6×6的随机数组
image = np.random.randint(0, 256, size=[6, 6], dtype=np.uint8)
w, h = image.shape # 得到数组的宽与高
# 建立新数组的大小
x = np.zeros((w, h), np.float32)
y = np.zeros((w, h), np.float32)
# 实现新数组的访问操作
for i in range(w):
    for j in range(h):
        x[(i, j)] = h - 1 - j
        y[(i, j)] = i
rst = cv.remap(image, x, y, cv.INTER_LINEAR) # 数组绕y轴翻转
# 打印输出结果
print("image=\n", image)
print("rst=\n", rst)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
image=
 [[182 211  25 119  17  24]
 [ 60  42 209 135 122 240]
 [ 25  19 225  67 112  18]
 [ 73  35 238 205 189 141]
 [249 179  11 129 115 138]
 [200  44 174  13  34   2]]
rst=
 [[ 24  17 119  25 211 182]
 [240 122 135 209  42  60]
 [ 18 112  67 225  19  25]
 [141 189 205 238  35  73]
 [138 115 129  11 179 249]
 [  2  34  13 174  44 200]]

绕x轴和y轴旋转

图像绕着x轴、y轴翻转，在数学上是指映射过程中，x坐标轴的值以y轴为对称轴进行交换，y坐标轴的值以x轴为对称轴进行交换。使用remap()函数实现时，map1的值设置为“总行数-1-当前行号”，map2的值设置为“总列数-1-当前列号”，这是由于OpenCV中行列号的下标是从0开始决定的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import cv2 as cv
import numpy as np
# 构建一个6×6的随机数组
image = np.random.randint(0, 256, size=[6, 6], dtype=np.uint8)
w, h = image.shape # 得到数组的宽与高
# 建立新数组的大小
x = np.zeros((w, h), np.float32)
y = np.zeros((w, h), np.float32)
# 实现新数组的访问操作
for i in range(w):
    for j in range(h):
        x[(i, j)] = h - 1 - j
        y[(i, j)] = w - 1 - i
rst = cv.remap(image, x, y, cv.INTER_LINEAR) # 数组绕x轴和y轴翻转
# 打印输出结果
print("image=\n", image)
print("rst=\n", rst)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
image=
 [[ 81  44 137 186  35 194]
 [  3 140  26  23 142 158]
 [237 155 158  90 173  11]
 [ 71  92  62  55 155   1]
 [175 218 234  63 240  34]
 [ 68 101 148 160 123 177]]
rst=
 [[177 123 160 148 101  68]
 [ 34 240  63 234 218 175]
 [  1 155  55  62  92  71]
 [ 11 173  90 158 155 237]
 [158 142  23  26 140   3]
 [194  35 186 137  44  81]]

投影变换

在仿射变换的过程中，物体的转换都是在二维空间中完成的，但是如果物体在三维空间中发生了转换，这种转换一般叫作投影变换。

原理简介

因为投影变换是在三维空间内进行的，所以对其进行修正十分困难。但是如果物体是平面的，那么就能通过二维投影变换对此物体三维变换进行模型化，这就是专用的二维投影变换，可由如下公式描述：

$$ \[\begin{pmatrix} \widetilde{x} \\ \widetilde{y} \\ \widetilde{z} \end{pmatrix}\] = \[\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}\] \[\begin{pmatrix} x \\ y \\ z \end{pmatrix}\]

$$

在OpenCV中提供了cv2.getPerspectiveTransform()函数来计算投影变换矩阵，其一般格式为：

1
cv2.getPerspectiveTransform(src,dst)
  • dst表示目标图像。
  • src表示原始图像。

注意 这里需要输入4组对应的坐标变换，src和dst分别是4×2的二维矩阵，其中每一行代表一个坐标，而且数据类型必须是32位浮点型，否则会报错。

Python实现

类似于仿射变换，OpenCV提供了cv2.warpPerspective()函数来实现投影变换功能，其一般格式为：

1
cv2.warpPerspective(src,M,dsize[,dst[,flags[,borderMode[,borderValue]]]])
  • src表示原始的图像。
  • M表示投影变换矩阵。
  • dsize表示投影后图像的大小。
  • flags表示插值方式。
  • borderMode表示边界模式。
  • borderValue表示边界值。

其使用方法与仿射变换相似，只是输入的变换矩阵变为3行3列的投影变换矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import cv2 as cv
import numpy as np
# 构建一个6×6的随机数组
image = cv.imread("pic/lena.png")
h, w = image.shape[:2]  # 得到数组的高与宽
# 原图像的4个需要变换的像素点
src = np.array([[0, 0], [w - 1, 0], [0, h - 1], [w - 1, h - 1]], np.float32)
# 投影变换的4个像素点
dst = np.array([[80, 80], [w/2, 50], [80, h - 80], [w - 40, h - 40]], np.float32)
M = cv.getPerspectiveTransform(src, dst)  # 计算出投影变换矩阵
# 进行投影变换
image1 = cv.warpPerspective(image, M, (w, h), borderValue=125)
# 显示图像
cv.imshow("image", image)
cv.imshow("image1", image1)
cv.waitKey()
cv.destroyAllWindows()
屏幕截图 2025-01-21 172342.png

极坐标变换

原理简介

笛卡尔坐标转极坐标

笛卡尔坐标系上\(xOy\)上任意一点\((x, y)\)，以\((\bar{x}, \bar{y})\)为中心，通过以下计算公式对应到极坐标系\(\theta o r\)：

\[ \begin{align} r = \sqrt{(x - \bar{x})^2 + (y - \bar{y})^2}, \\ \theta = \begin{cases} 2{\rm \pi} & y - \bar{y} \leq 0, \\ \arctan2(x - \bar{x}, y - \bar{y}) & y - \bar{y} > 0. \\ \end{cases} \end{align} \]

上式中，θ的取值范围用角度表示为0～360°，反正切函数\(\arctan2\)返回的角度和笛卡儿坐标点所在的象限有关，如果\((x - \bar{x}, y - \bar{y})\)在第一象限，反正切的角度范围为0～90°；如果在第二象限，反正切的角度范围为90°～180°；如果在第三象限，反正切的角度范围为-180°～-90°；如果在第四象限，反正切的角度范围为-90°～0°。通常将\(y - \bar{y} \leq 0\)时返回的正切角度加上一个周期360°，所以经过极坐标变换后的角度范围为0～360°。

极坐标转笛卡尔坐标

在已知极坐标\((\theta, r)\)和笛卡尔坐标\((\bar{x}, \bar{y})\)的条件下，计算笛卡尔坐标\((x, y)\)以\((\bar{x}, \bar{y})\)为中心的极坐标变换是\((\theta, r)\)，可通过一下公式计算：

\[ \begin{align} x = \bar{x} + r\cos\theta, \\ y = \bar{y} + r\sin\theta. \end{align} \]

Python实现

在OpenCV中提供了两种进行极坐标变换的函数，分别是linearPolar()函数和logPolar()函数，其中linearPolar()函数的一般格式为：

1
cv2.linearPolar(src, dst, center, maxRadius, flags)
  • src表示原始的图像。
  • dst表示输出图像。
  • center表示极坐标变换中心。
  • maxRadius表示极坐标变换的最大距离。
  • flags表示插值算法。

logPolar()函数的一般格式为：

1
cv2.logPolar(src, dst, center, M, flags)
  • src表示原始的图像。
  • dst表示输出图像。
  • center表示极坐标变换中心。
  • M表示极坐标变换的系数。
  • flags表示转换的方向。

例如，使用linearPolar()：

1
2
3
4
5
6
7
8
9
10
import cv2 as cv

image = cv.imread("pic/circles.png", cv.IMREAD_ANYCOLOR)
# 参数设置
dst = cv.linearPolar(image, (251, 249), 225, cv.INTER_LINEAR)
# 显示图像
cv.imshow("image", image)
cv.imshow("dst", dst)
cv.waitKey()
cv.destroyAllWindows()

使用logPolar()：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import cv2 as cv

image = cv.imread("pic/circles.png", cv.IMREAD_ANYCOLOR)
# 设置参数，实现极坐标变换
M1 = 20
M2 = 50
M3 = 90
# 笛卡儿坐标向极坐标转换
dst1 = cv.logPolar(image, (251, 249), M1, cv.WARP_FILL_OUTLIERS)
dst2 = cv.logPolar(image, (251, 249), M2, cv.WARP_FILL_OUTLIERS)
dst3 = cv.logPolar(image, (251, 249), M3, cv.WARP_FILL_OUTLIERS)
# 显示图像
cv.imshow("image", image)
cv.imshow("dst1", dst1)
cv.imshow("dst2", dst2)
cv.imshow("dst3", dst3)
cv.waitKey()
cv.destroyAllWindows()